• author: zhouyongsdzh@foxmail.com
• date: 2017-06-08
• weibo: @周永_52ML

---

目录

• 写在前面
• 词向量

写在前面

在第四章：循环神经网络一章中讲到了神经语言模型，神经语言模型第一层是embedding映射，然后是全连接操作。embedding映射就是将一个词（CTR预估模型中经常是ID型特征）映射为一个$k$维的实数值向量。

在NLP任务中，我们将自然语言交给机器学习（或深度学习）算法来处理，但机器无法直接理解这些数据或语言，因此首先要做的是将语言数学化，如何对自然语言进行数学化呢？词向量是一种很好的方式。

词向量

通常词向量有两种表示方式，一种是One-hot Representation，另一种是Distributed Representation。

One-hot比较好理解，不过多赘述，它有一些缺点，如容易受维数灾难的困扰，尤其是将其用于深度学习场景时；在NLP场景中，它还不能刻画词与词之间的相似性。

Distributed Representation最早是Hinton于1986年提出的，它可以克服one hot表示的缺点，其基本思想：通过训练将某种语言中的每一个词映射成一个固定长度的向量，所有的向量构成词向量空间，而每一向量可视为该空间中的一个点，在这个空间上引入“距离”，就可以根据词之间的距离来判断它们之间相似性了。

为什么叫Distributed Representation（分布式表示）呢？一个理解是：对于one-hot presentation，向量中只有一个非零值，非常集中；而对于Distributed Representation表示的向量有大量非零值，相对分散，把词的信息分布到各个分量中去了。

注意：词向量只是针对“词”来提的，事实上，我们也可以针对更细粒度或更粗粒度进行推广，如字向量（charactor-level），句子向量或文档向量等。

目前，词向量学习方法中比较主流有word2vec，glove，fasttext和elmo，还有基于char-level的Bi-LSTM方法、CNN＋Highway NN + LSTM等方法。我们先从word2vec开始介绍。

word2vec有两种不同的建模方式，分别称为CBOW模型和Skip-gram模型。

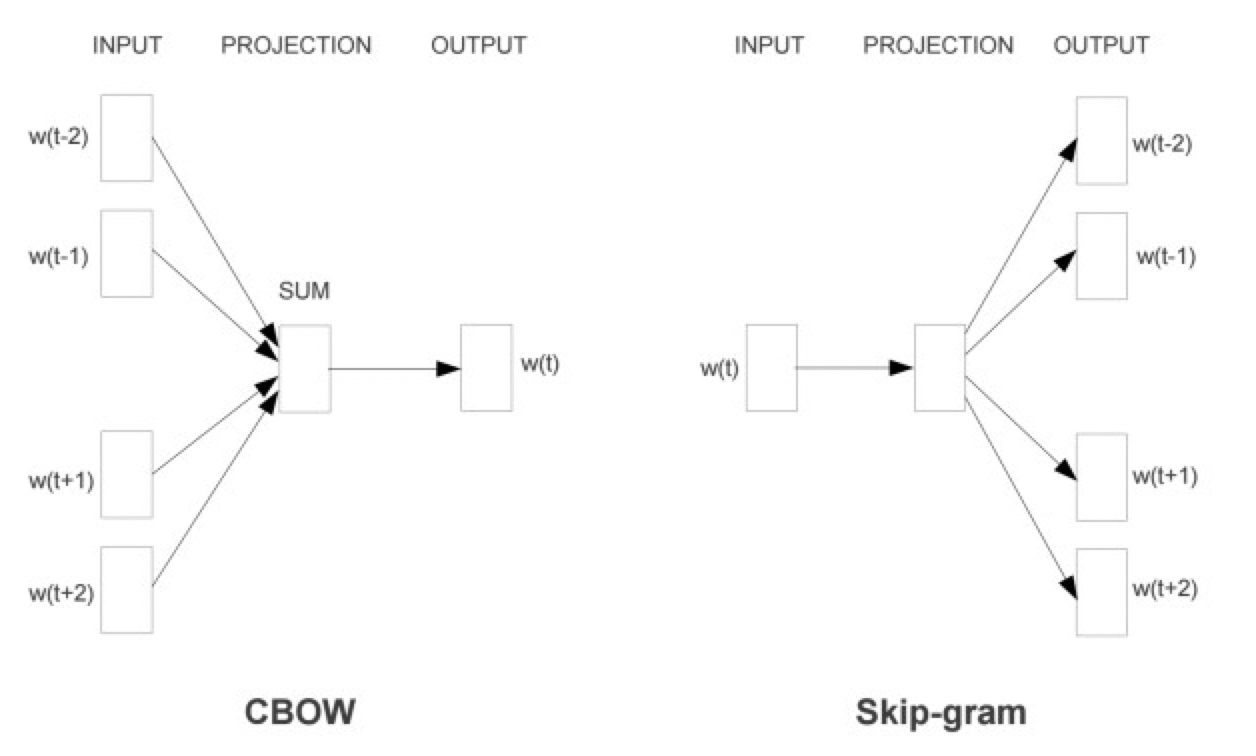
由图可见，两个模型都包含3层结构：输入层、映射层和输出层。cbow模型是在已知当前词$w_t$的上下文$w_{t-2},w_{t-1},w_{t+1},w_{t+2}$的前提下预测当前词$w_t$；skip-gram模型恰恰相反，是在遗址当前词$w_t$的前提下，预测其上下文$w_{t-2},w_{t-1},w_{t+1},w_{t+2}$。

对于这两个模型结构，word2vec论文中提供了两套学习框架，分别是Herarchical Softmax和Negative Sampling来进行学习。

小结：两种建模方式对应着两种不同的条件概率，学习框架具体地表示了条件概率函数。

word2vec模型

基于Hierarchical Softmax算法的word2vec模型

在第4章中我们提到，基于神经网络的语言模型的目标函数通常优化其对数似然函数：

$$
\mathcal{L} = \sum_{w \in C} \log p(w | context(w))
$$

其中的关键是条件概率函数$p(w | context(w))$的构造，n-gram模型中给出了一种构造方法。对于word2vec中基于分层Softmax的cbow模型，优化的目标函数也如上式；而对于基于分层softmax的Skip-gram模型，优化的目标函数则形如：

$$
\mathcal{L} = \sum_{w \in C} \log p(context(w) | w)
$$

因此，下面我们重点关注两个条件概率模型是如何构造的？

cbow模型结构

基于HS的cbow模型的网络结构示意图如下：

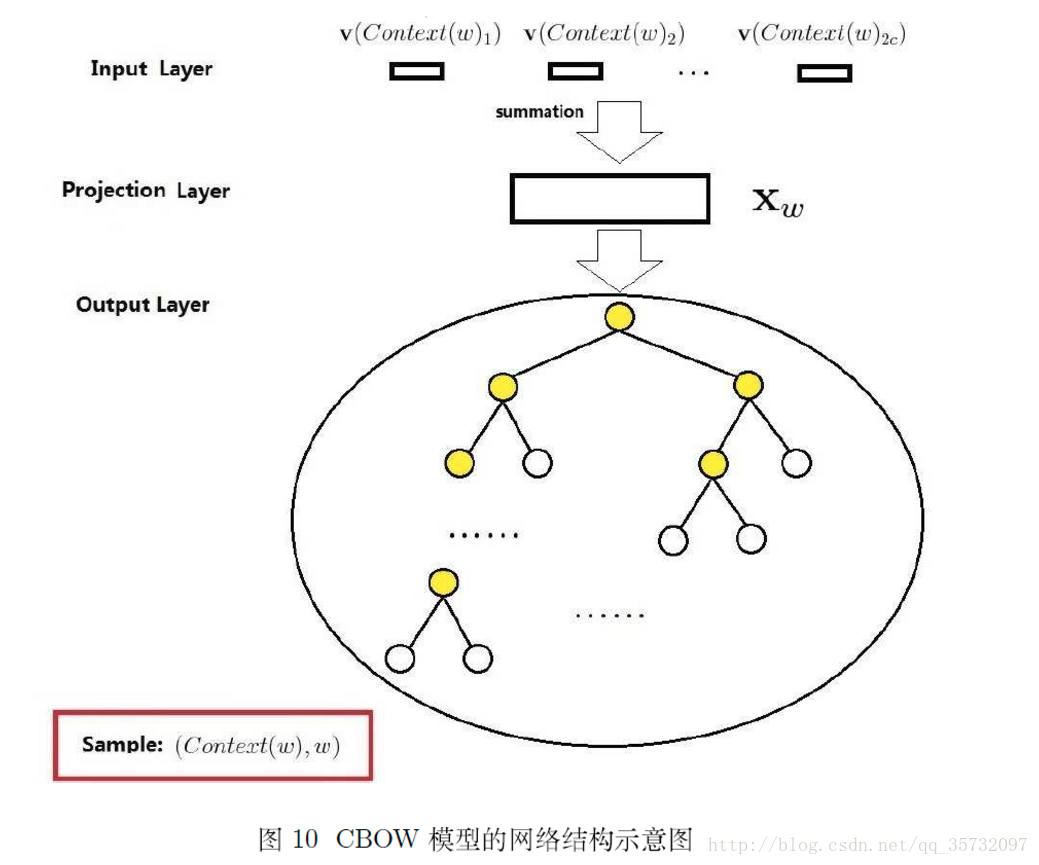
• 输入层

包含context(w)中2c个词的词向量$v(context(w)_1),v(context(w)_2),\cdots,v(context(w)_{2c}) \in R^k$，这里$k$表示词向量的长度。

• 映射层

cbow投影层比较简单，将输入层的2c个词向量做求和累加，即$x_w = \sum_{i=1}^{2c} v(context(w)_i) \in R^k$

• 输出层

输出层对应一颗二叉树，它是以语料中出现过的词当叶子节点，以各词在语料中出现的次数当权重构造出来的Huffman树。这棵Huffman树中，叶子节点共有N个，分别对应词典$\mathcal{D}$中的词，非叶子节点N-1个。

相对于第4章的神经网络语言模型结构，基于cbow模型的结构有3点不同：1.输入层到映射层的操作，前者是concat，后者是sum；2. 前者有隐藏层，后者无隐藏层；3. 输出层方面，前者是线性模型，后者是树形结构（Huffmans树）。

cbow模型表达

Herarchical Softmax是提高word2vec模型训练性能的重要技术，为了描述方便，先定义一些符号，假设huffman树中的某个叶子节点对应词典$\mathcal{D}$中的词$w$，定义：

符号	含义
$p^{w}$	从根节点出发到达$w$叶子节点的对应路径
$l^w$	路径$p^w$中包含节点的个数
$p_1^w,p_2^w,\cdots,p_{l^w}^{w}$	路径$p^w$中的$l^w$个节点，其中$p_1^w$表示根节点，$p_{l^w}^w$表示词$w$对应的节点
$d_2^w,d_3^w,\cdots,d_{l^w}^w \in \{0,1\}$	词$w$的huffman编码，它由$l^w-1$位编码构成，$d_j^w$表示路径$p^w$中第$j$个节点对应的编码（根节点不对应编码）
$\theta_1^w,\theta_2^w,\cdots,\theta_{l^w - 1}^w \in R^k$	路径$p^w$中非叶子节点对应的向量，$\theta_j^w$表示路径$p^w$中第$j$个非叶子节点对应的向量。

word2vec模型最后得到的是词典$\mathcal{D}$中每个词的向量，这里为什么还要为huffman树非叶子节点也定义个向量呢？这里它只是辅助向量，相当于中间变量。

// TODO 补充

基于HS的cbow模型的条件概率函数为：

$$
p(w|context(w)) = \prod_{j=2}^{l^w} p(d_j^w | x_w, \theta_{j-1}^w)
$$

其中

$$
p(d_j^w | x_w, \theta_{j-1}^w) =
\begin{cases} \sigma(x_w^T \theta_{j-1}^w), \quad & d_j^w = 0, \\\
1-\sigma(x_w^T \theta_{j-1}^w) \quad & d_j^w=1
\end{cases}
$$

写成整体的表达式为:

$$
p(w|context(w)) = \prod_{j=2}^{l^w} \left[ \sigma(x_w^T \theta_{j-1}^w) \right]^{1-d_j^w} \cdot \left[ 1-\sigma(x_w^T \theta_{j-1}^w) \right]^{d_j^w}
$$

注意：这里是基于HS的cbow模型表达式，笔者经常用该题目考察候选人对word2vec的理解程度，但仅有十之一二能给出正确答案。

梯度计算

那么基于HS的cbow模型的目标函数（似然函数的对数形式）整理为：

$$
\begin{align}
\mathcal{L} &= \sum_{w \in \mathcal{C}} \log p(w|context(w)) \\\
&= \sum_{w \in \mathcal{C}} \sum_{j=2}^{l^w} \left\{ (1 - d_j^w) \log\left(\sigma(x_w^T \theta_{j-1}^w)\right) + d_j^w \log \left(1-\sigma(x_w^T \theta_{j-1}^w) \right) \right\}
\end{align}
$$

优化目标中的参数有$x_w, \theta_{j-1}^w$。如何最大化目标函数，word2vec工具使用的是随机梯度提升法，前提先算法出优化目标对参数的梯度表达式。为公式推导方便，即花括号里的公式为$\mathcal{L}(w, j)$，分别对参数$x_w, \theta_{j-1}^w$求导：

$$
\begin{align}
\frac{\partial \mathcal{L}(w,j)}{\partial \theta_{j-1}^w}
&= \frac{\partial}{\partial \theta_{j-1}^w} \left\{ (1 - d_j^w) \log\left(\sigma(x_w^T \theta_{j-1}^w)\right) + d_j^w \log \left(1-\sigma(x_w^T \theta_{j-1}^w) \right) \right\} \\\
&= (1-d_j^w) \left(1-\sigma(x_w^T \theta_{j-1}^w) \right)x_w - d_j^w \sigma(x_w^T \theta_{j-1}^w)x_w \\\
&= \left(1 - \sigma(x_w^T \theta_{j-1}^w) - d_j^w \right) x_w
\end{align}
$$

于是，参数$\theta_{j-1}^w$的更新公式为：

$$
\theta_{j-1}^w \leftarrow \theta_{j-1}^w + \eta \left(1 - \sigma(x_w^T \theta_{j-1}^w) - d_j^w \right) x_w
$$

对于参数$x_w$的梯度，可以根据变量的对称性（两者可交换位置）得到。即相应的梯度$\frac{\partial \mathcal{L}(w,j)}{\partial x_w}$只需在梯度$\frac{\partial \mathcal{L}(w,j)}{\partial \theta_{j-1}^w}$的基础上对两个参数交换位置就可以了，即

$$
\frac{\partial \mathcal{L}(w,j)}{\partial x_w} = \left(1 - \sigma(x_w^T \theta_{j-1}^w) - d_j^w \right) \theta_{j-1}^w
$$

参数$x_w$的更新公式类似$\theta_{j-1}^w$的公式，不再赘述。那么，对每个词的向量$v(\hat{w}), \hat{w} \in context(w)$，其更新公式为：

$$
v(\hat{w}) \leftarrow v(\hat{w}) + \eta \sum_{j=2}^{l^w} \left(1 - \sigma(x_w^T \theta_{j-1}^w) - d_j^w \right) \theta_{j-1}^w
$$

基于Hierarchical Softmax的skip-gram模型

skip-gram模型结构

与cbow模型一样，基于hs的skip-gram输出层也是Huffman树。

$$
\begin{align}
p(context(w)|w)
&= \prod_{u \in context(w)} p(u|w) \\\
&= \prod_{u \in context(w)} \prod_{j=2}^{l^w} p(d_j^u | v_w, \theta_{j-1}^u) \\\
&= \prod_{u \in context(w)} \prod_{j=2}^{l^w} \left[\sigma(v_w \theta_{j-1}^u)\right]^{1-d_j^u} \cdot \left[1 - \sigma(v_w \theta_{j-1}^u)\right]^{d_j^u}
\end{align}
$$

目标函数：

$$
\begin{align}
\mathcal{L}
&= \sum_{w \in C} \log p(context(w)|w) \\\
&= \sum_{w \in C} \sum_{u \in context(w)} \sum_{j=2}^{l^u} \left\{ (1 - d_j^u) \log \left(\sigma(v_w\theta_{j-1}^u)\right) + d_j^u \log \left(1 - \sigma(v_w\theta_{j-1}^u)\right) \right\}
\end{align}
$$

为了梯度公式推导方便，我们把三重花括号里的公式记为$\mathcal{L}(w,u,j)$，公式为：

$$
\mathcal{L}(w,u,j) = (1 - d_j^u) \log \left(\sigma(v_w\theta_{j-1}^u)\right) + d_j^u \log \left(1 - \sigma(v_w\theta_{j-1}^u)\right)
$$

以上就是基于HS的skip-gram模型的优化目标。下面分别对参数$v_w, \theta_{j-1}^u$求导，

$$
\frac{\partial \mathcal{L}(w,u,j)} {\partial v_w} = \left(1 - d_j^u - \sigma(v_w \theta_{j-1}^u) \right) \theta_{j-1}^u
$$

因此，可得参数$v_w$的更新公式为：

$$
v_w \leftarrow v_w + \eta \sum_{u \in context(w)} \sum_{j=2}^{l^u} \left(1 -d_j^u - \sigma(v_w \theta_{j-1}^u) \right) \theta_{j-1}^u
$$

同样的，根据参数对称性，可得参数$\theta_{j-1}^u$的更新公式为：

$$
\theta_{j-1}^u \leftarrow \theta_{j-1}^u + \eta \left(1 - d_j^u - \sigma(v_w \theta_{j-1}^u) \right) v_w
$$

在Google word2vec源码对于$v_w$的更新并不是在两层for循环外才更新，而是每处理一个词后更新$v_w$参数。

基于Negative Sample算法的word2vec模型

cbow模型

cbow模型是已知上下文$context(w)$预测中心词$w$。因此，对于给定的$context(w)$，词$w$就是一个正样本，其它词就是负样本了。

负样本如此多，该如何选取呢？该问题相对独立，后面会单独介绍。

假定现在已经选好了一个关于词$w$的负样本子集$NEG(w) \neq \emptyset$，且对于$\forall \hat{w} \in \mathcal{D}$，定义：

$$
L^w(\hat{w}) = \begin{cases}
1, \quad \hat{w} = w; \\\
0, \quad \hat{w} \neq w
\end{cases}
$$

$L^w(\hat{w})$表示词的标签，正样本标签为1，负样本标签为0.

对于一个给定的正样本，我们希望最大化：

$$
g(w) = \prod_{u \in {w} \cup NEG(w)} p(u | context(w))
$$

概率公式为：

$$
p(u|context(w)) =
\begin{cases}
\sigma(x_w^T \theta^u) & \quad L^w(u) = 1, \\\
1 - \sigma(x_w^T \theta^u) & \quad L^w(u) \neq 1
\end{cases}
$$

这里$x_w$仍然表示上下文向量之和，$\theta^u \in R^m$是词u对应的一个辅助向量，待训练参数。把上式整理为一个完整的表达式为：

$$
g(w) = \prod_{u \in w \cup NEG(w)} \left[\sigma(x_w^T \theta^u) \right]^{L^w(u)} \cdot \left[1 - \sigma(x_w^T \theta^u) \right]^{1 - L^w(u)}
$$

那么，为什么要最大化$g(w)$呢？我们再整理一下上式：

$$
g(w) = \sigma(x_w^T \theta^w) \prod_{u \in NEG(w)} \left[1- \sigma(x_w^T \theta^u) \right]
$$

$\sigma(x_w^T \theta^w)$表示当上下文为context(w)时，预测中心词为w的概率。$\sigma(x_w^T \theta^u), u \in NEG(w)$表示当上下文为context(w)时，预测中心词为u的概率。从形式上看，最大化$g(w)$等价于最大化$\sigma(x_w^T \theta^w)$同时最小化所有的$\sigma(x_w^T \theta^u)$，这正是我们所希望的：最大化正样本的概率同时最小化负样本的概率。

于是，对于给定的一个语料库$C$，优化目标为：

$$
G = \prod_{w \in C} g(w)
$$

基于Negative Sample算法的word2vec模型