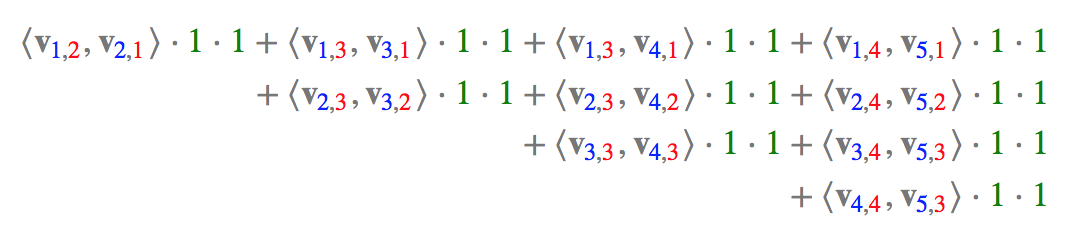第09章：深入浅出ML之Factorization家族

文章目录

1. 写在前面
2. 因子分解机
3. 场感知分解机
1. 3.1. FFM应用场景
2. 3.2. 参考资料

author: zhouyongsdzh@foxmail.com
date: 2015-12-18
weibo: @周永_52ML

内容列表

写在前面
Factorization Machine
Field-aware Factorization Machine

写在前面

因子分解机

因子分解机（Factorization Machine，简称FM），又称分解机器。是由Konstanz大学（德国康斯坦茨大学）Steffen Rendle（现任职于Google）于2010年最早提出的，旨在解决大规模稀疏数据下的特征组合问题。在系统介绍FM之前，我们先了解一下在实际应用场景中，稀疏数据是怎样产生的？

用户在网站上的行为数据会被Server端以日志的形式记录下来，这些数据通常会存放在多台存储机器的硬盘上。

以我浪为例，各产品线纪录的用户行为日志会通过flume等日志收集工具交给数据中心托管，它们负责把数据定时上传至HDFS上，或者由数据中心生成Hive表。

我们会发现日志中大多数出现的特征是categorical类型的，这种特征类型的取值仅仅是一个标识，本身并没有实际意义，更不能用其取值比较大小。比如日志中记录了用户访问的频道（channel）信息，如”news”, “auto”, “finance”等。

假设channel特征有10个取值，分别为$\{\text{“auto”}, \text{“finance”}, \text{“ent”}, \text{“news”}, \text{“sports”}, \text{“mil”}, \text{“weather”}, \text{“house”}, \text{“edu”}, \text{“games”} \}$。部分训练数据如下：

user channel

user1 sports

user2 news

user3 finance

user4 house

user5 edu

user6 news

… …

user	channel
user1	sports
user2	news
user3	finance
user4	house
user5	edu
user6	news
…	…

特征ETL过程中，需要对categorical型特征进行one-hot编码（独热编码），即将categorical型特征转化为数值型特征。channel特征转化后的结果如下：

user chn-auto chn-finance chn-ent chn-news chn-sports chn-mil chn-weather chn-house chn-edu chn-games

user1 0 0 0 0 1 0 0 0 0 0

user2 0 0 0 1 0 0 0 0 0 0

user3 0 1 0 0 0 0 0 0 0 0

user4 0 0 0 0 0 0 0 1 0 0

user5 0 0 0 0 0 0 0 0 1 0

user6 0 0 0 1 0 0 0 0 0 0

user	chn-finance	chn-news	chn-sports	chn-house	chn-edu
user1	0	0	1	0	0
user2	0	1	0	0	0
user3	1	0	0	0	0
user4	0	0	0	1	0
user5	0	0	0	0	1
user6	0	1	0	0	0

可以发现，由one-hot编码带来的数据稀疏性会导致特征空间变大。上面的例子中，一维categorical特征在经过one-hot编码后变成了10维数值型特征。真实应用场景中，未编码前特征总维度可能仅有数十维或者到数百维的categorical型特征，经过one-hot编码后，达到数千万、数亿甚至更高维度的数值特征在业内都是常有的。

我组广告和推荐业务的点击预估系统，编码前是特征不到100维，编码后（包括feature hashing）的维度达百万维量级。

此外也能发现，特征空间增长的维度取决于categorical型特征的取值个数。在数据稀疏性的现实情况下，我们如何去利用这些特征来提升learning performance？

或许在学习过程中考虑特征之间的关联信息。针对特征关联，我们需要讨论两个问题：1. 为什么要考虑特征之间的关联信息？2. 如何表达特征之间的关联？

为什么要考虑特征之间的关联信息？

大量的研究和实际数据分析结果表明：某些特征之间的关联信息（相关度）对事件结果的的发生会产生很大的影响。从实际业务线的广告点击数据分析来看，也正式了这样的结论。
如何表达特征之间的关联？

表示特征之间的关联，最直接的方法的是构造组合特征。样本中特征之间的关联信息在one-hot编码和浅层学习模型（如LR、SVM）是做不到的。目前工业界主要有两种手段得到组合特征：
1. 人工特征工程（数据分析＋人工构造）；
2. 通过模型做组合特征的学习（深度学习方法、FM/FFM方法）

本章主要讨论FM和FFM用来学习特征之间的关联。我们在《第01章：深入浅出ML之Regression家族》看到的多项式回归模型，其中的交叉因子项$x_i x_j$就是组合特征最直观的例子。

$x_i x_j$表示特征$x_i$和$x_j$的组合，当$x_i$和$x_j$都非零时，组合特征$x_i x_j$才有意义。

这里我们以二阶多项式模型（degree=2时）为例，来分析和探讨FM原理和参数学习过程。

FM模型表达

为了更好的介绍FM模型，我们先从多项式回归、交叉组合特征说起，然后自然地过度到FM模型。

二阶多项式回归模型

我们先看二阶多项式模型的表达式：

$$
\hat{y}(x) := \underbrace {w_0 + \sum_{i=1}^{n} w_i x_i }_{\text{线性回归}} + \underbrace {\sum_{i=1}^{n} \sum_{j=i+1}^{n} w_{ij} x_i x_j}_{\text{交叉项（组合特征）}} \qquad \text{(n.ml.1.9.1)}
$$

其中，$n$表示样本特征维度，截距$w_0 \in R,\; w ＝ \{w_1, w_2, \cdots, w_n\}\in R^n, w_{ij} \in R^{n \times n}$为模型参数。

从公式$\text{(n.ml.1.9.1)}$可知，交叉项中的组合特征参数总共有$\frac{n(n-1)}{2}$个。在这里，任意两个交叉项参数$w_{ij}$都是独立的。然而，在数据非常稀疏的实际应用场景中，交叉项参数的学习是很困难的。why？

因为我们知道，回归模型的参数$w$的学习结果就是从训练样本中计算充分统计量（凡是符合指数族分布的模型都具有此性质），而在这里交叉项的每一个参数$w_{ij}$的学习过程需要大量的$x_i、x_j$同时非零的训练样本数据。由于样本数据本来就很稀疏，能够满足“$x_i$和$x_j$都非零”的样本数就会更少。训练样本不充分，学到的参数$w_{ij}$就不是充分统计量结果，导致参数$w_{ij}$不准确，而这会严重影响模型预测的效果（performance）和稳定性。How to do it ?

那么，如何在降低数据稀疏问题给模型性能带来的重大影响的同时，有效地解决二阶交叉项参数的学习问题呢？矩阵分解方法已经给出了解决思路。这里借用CMU讨论课中提到的FM课件和美团－深入FFM原理与实践中提到的矩阵分解例子（美团技术团队的分享很赞👍）。

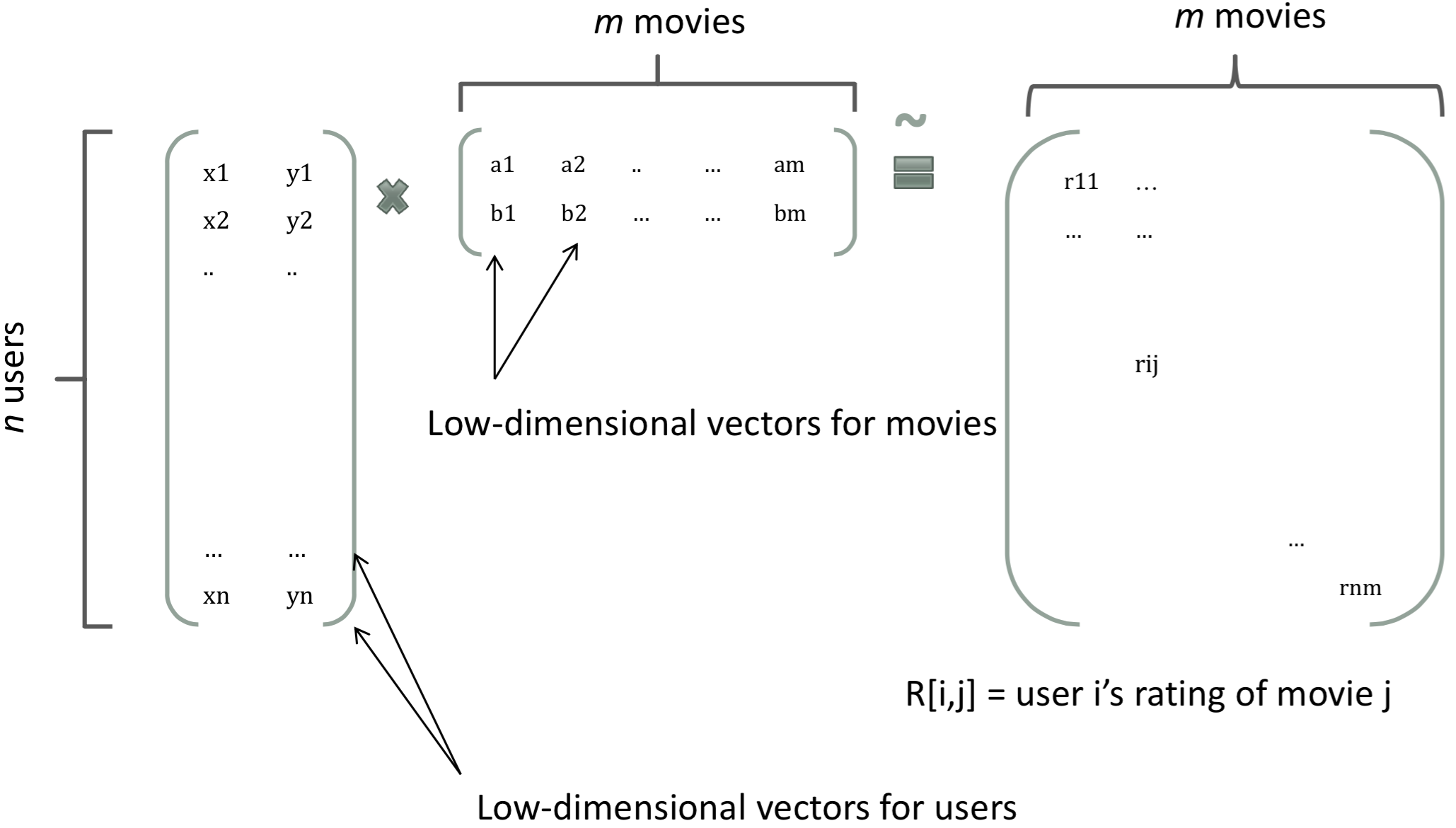
在基于Model-Based的协同过滤中，一个rating矩阵可以分解为user矩阵和item矩阵，每个user和item都可以采用一个隐向量表示。如下图所示。

上图把每一个user表示成了一个二维向量，同时也把item表示成一个二维向量，两个向量的内积就是矩阵中user对item的打分。

根据矩阵分解的启发，如果把多项式模型中二阶交叉项参数$w_{ij}$组成一个对称矩阵$W$（对角元素设为正实数），那么这个矩阵就可以分解为$W = V V^T$，$V \in R^{n \times k}$称为系数矩阵，其中第$i$行对应着第$i$维特征的隐向量 (这部分在FM公式解读中详细介绍)。

将每个交叉项参数$w_{ij}$用隐向量的内积$\langle \mathbf{v}_i, \mathbf{v}_j\rangle$表示，是FM模型的核心思想。下面对FM模型表达式和参数求解过程，给出详细解读。

FM模型表达

这里我们只讨论二阶FM模型（degree＝2），其表达式为：

$$
\hat{y}(\mathbf{x}) := w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j \qquad \text{(ml.1.9.1)}
$$

其中，$\mathbf{v}_i$表示第$i$特征的隐向量，$\langle \cdot, \cdot\rangle$表示两个长度为$k$的向量的内积，计算公式为：

$$
\langle \mathbf{v}_i, \mathbf{v}_j \rangle := \sum_{f=1}^{k} v_{i,f} \cdot v_{j,f} \qquad \text{(ml.1.9.2)}
$$

公式解读：

线性模型＋交叉项

直观地看FM模型表达式，前两项是线性回归模型的表达式，最后一项是二阶特征交叉项（又称组合特征项），表示模型将两个互异的特征分量之间的关联信息考虑进来。用交叉项表示组合特征，从而建立特征与结果之间的非线性关系。

交叉项系数 $\to$ 隐向量内积

由于FM模型是在线性回归基础上加入了特征交叉项，模型求解时不直接求特征交叉项的系数$w_{ij}$（因为对应的组合特征数据稀疏，参数学习不充分），故而采用隐向量的内积$\langle \mathbf{v}_i, \mathbf{v}_j\rangle$表示$w_{ij}$。

具体的，FM求解过程中的做法是：对每一个特征分量$x_i$引入**隐向量$\mathbf{v}_i ＝ (v_{i,1}, v_{i,2}, \cdots, v_{i,k})$**，利用$v_i v_j^T$内积结果对交叉项的系数$w_{ij}$进行估计，公式表示：$\hat{w}_{ij} := v_i v_j^T$.

隐向量的长度$k$称为超参数$(k \in N^+, k \ll n)$，$\mathbf{v}_i = (v_{i,1}, v_{i,2}, \cdots, v_{i,k})$的含义是用$k$个描述特征的因子来表示第$i$维特征。根据公式$\text{(ml.1.9.1)}$，二阶交叉项的参数由$n \cdot n$个减少到$n \cdot k$个，远少于二阶多项式模型中的参数数量。

此外，参数因子化表示后，使得$x_h x_i$的参数与$x_i x_j$的参数不再相互独立。这样我们就可以在样本稀疏情况下相对合理的估计FM模型交叉项的参数。具体地：

$$
\begin{align}
\langle \mathbf{v}_h, \mathbf{v}_i \rangle &:= \sum_{f=1}^{k} v_{h,f} \cdot v_{i,f} \quad(1)\\
\langle \mathbf{v}_i, \mathbf{v}_j \rangle &:= \sum_{f=1}^{k} v_{i,f} \cdot v_{j,f} \;\quad(2)
\end{align} \qquad (n.ml.1.9.2)
$$

$x_h x_i$与$x_i x_j$的系数分别为$\langle \mathbf{v}_h, \mathbf{v}_i \rangle$和$\langle \mathbf{v}_i, \mathbf{v}_j \rangle$，他们之间有共同项$\mathbf{v}_i$。也就是说，所有包含$x_i$的非零组合特征（存在某个$j \neq i$，使得$x_ix_j \neq 0$）的样本都可以用来学习隐向量$\mathbf{v}_i$，这在很大程度上避免了数据稀疏行造成参数估计不准确的影响。

在二阶多项式模型中，参数$w_{hi}$和$w_{ij}$的学习过程是相互独立的。

论文中还提到FM模型的应用场景，并且说公式$\text{(ml.1.9.1)}$作为一个通用的拟合模型（Generic Model），可以采用不同的损失函数来解决具体问题。比如：

FM应用场景	损失函数	说明
回归	均方误差（MSE）损失	Mean Square Error，与平方误差类似
二类分类	Hinge/Cross-Entopy损失	分类时，结果需要做sigmoid变换
排序	.	.

FM参数学习

等式变换

公式$\text{(ml.1.9.1)}$中直观地看，FM模型的复杂度为$O(kn^2)$，但是通过下面的等价转换，可以将FM的二次项化简，其复杂度可优化到$O(kn)$。即：

$$
\sum_{i=1}^{n} \sum_{j=i+1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_j \rangle} x_i x_j = \frac{1}{2} \sum_{f=1}^{k} {\left \lgroup \left(\sum_{i=1}^{n} v_{i,f} x_i \right)^2 - \sum_{i=1}^{n} v_{i,f}^2 x_i^2\right \rgroup} \qquad(ml.1.9.3)
$$

下面给出详细推导：

$$
\begin{align}
& \sum_{i=1}^{n} \sum_{j=i+1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_j \rangle} x_i x_j \qquad\qquad\qquad\qquad\qquad\qquad(1)\\
= & \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_j \rangle} x_i x_j - \frac{1}{2} \sum_{i=1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_i \rangle} x_i x_i \qquad\qquad\;\;(2)\\
= & \frac{1}{2} \left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i,f} v_{j,f} x_i x_j - \sum_{i=1}^{n} \sum_{f=1}^{k} v_{i,f} v_{i,f} x_i x_i \right) \qquad\,(3) \\
= & \frac{1}{2} \sum_{f=1}^{k} {\left \lgroup \left(\sum_{i=1}^{n} v_{i,f} x_i \right) \cdot \left(\sum_{j=1}^{n} v_{j,f} x_j \right) - \sum_{i=1}^{n} v_{i,f}^2 x_i^2 \right \rgroup} \quad\;\;\,(4) \\
= & \frac{1}{2} \sum_{f=1}^{k} {\left \lgroup \left(\sum_{i=1}^{n} v_{i,f} x_i \right)^2 - \sum_{i=1}^{n} v_{i,f}^2 x_i^2\right \rgroup} \qquad\qquad\qquad\;\;(5)
\end{align} \qquad(n.ml.1.9.3)
$$

解读第（1）步到第（2）步，这里用$A$表示系数矩阵$V$的上三角元素，$B$表示对角线上的交叉项系数。由于系数矩阵$V$是一个对称阵，所以下三角与上三角相等，有下式成立：

$$
A = \frac{1}{2} (2A+B) - \frac{1}{2} B. \quad \underline{ A=\sum_{i=1}^{n} \sum_{j=i+1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_j \rangle} x_i x_j } ; \quad \underline{ B = \frac{1}{2} \sum_{i=1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_i \rangle} x_i x_i } \quad (n.ml.1.9.4)
$$

如果用随机梯度下降（Stochastic Gradient Descent）法学习模型参数。那么，模型各个参数的梯度如下：

$$
\frac{\partial}{\partial \theta} y(\mathbf{x}) =
\left \{
\begin{array}{ll}
1, & \text{if}\; \theta\; \text{is}\; w_0 \qquad \text{(常数项)} \\
x_i & \text{if}\; \theta\; \text{is}\; w_i \;\qquad \text{(线性项)} \\
x_i \sum_{j=1}^{n} v_{j,f} x_j - v_{i,f} x_i^2, & \text{if}\; \theta\; \text{is}\; v_{i,f} \qquad \text{(交叉项)}
\end{array}
\right. \qquad\quad(ml.1.9.4)
$$

其中， $v_{j,f}$是隐向量$\mathbf{v}_j$的第$f$个元素。

梯度法训练FM

给出伪代码

FM训练复杂度

由于$\sum_{j=1}^{n} v_{j,f} x_j$只与$f$有关，在参数迭代过程中，只需要计算第一次所有$f$的$\sum_{j=1}^{n} v_{j,f} x_j$，就能够方便地得到所有$v_{i,f}$的梯度。显然，计算所有$f$的$\sum_{j=1}^{n} v_{j,f} x_j$的复杂度是$O(kn)$；已知$\sum_{j=1}^{n} v_{j,f} x_j$时，计算每个参数梯度的复杂度是$O(n)$；得到梯度后，更新每个参数的复杂度是 $O(1)$；模型参数一共有$nk + n + 1$个。因此，FM参数训练的时间复杂度为$O(kn)$。

综上可知，FM算法可以在线性时间内完成模型训练，以及对新样本做出预测，所以说FM是一个非常高效的模型。

FM总结

上面我们主要是从FM模型引入（多项式开始）、模型表达和参数学习的角度介绍的FM模型，这里我把我认为FM最核心的精髓和价值总结出来，与大家讨论。FM模型的核心作用可以概括为以下3个：

1. FM降低了交叉项参数学习不充分的影响

one-hot编码后的样本数据非常稀疏，组合特征更是如此。为了解决交叉项参数学习不充分、导致模型有偏或不稳定的问题。作者借鉴矩阵分解的思路：每一维特征用$k$维的隐向量表示，交叉项的参数$w_{ij}$用对应特征隐向量的内积表示，即$\langle \mathbf{v}_i, \mathbf{v}_j \rangle$（也可以理解为平滑技术）。这样参数学习由之前学习交叉项参数$w_{ij}$的过程，转变为学习$n$个单特征对应$k$维隐向量的过程。

很明显，单特征参数（$k$维隐向量$\mathbf{v}_i$）的学习要比交叉项参数$w_{ij}$学习得更充分。示例说明：

假如有10w条训练样本，其中出现女性特征的样本数为3w，出现男性特征的样本数为7w，出现汽车特征的样本数为2000，出现化妆品的样本数为1000。特征共现的样本数如下：

共现交叉特征样本数注

<女性，汽车> 500 同时出现<女性，汽车>的样本数

<女性，化妆品> 1000 同时出现<女性，化妆品>的样本数

<男性，汽车> 1500 同时出现<男性，汽车>的样本数

<男性，化妆品> 0 样本中无此特征组合项

共现交叉特征	样本数	注
`<女性，汽车>`	500	同时出现`<女性，汽车>`的样本数
`<女性，化妆品>`	1000	同时出现`<女性，化妆品>`的样本数
`<男性，汽车>`	1500	同时出现`<男性，汽车>`的样本数
`<男性，化妆品>`	0	样本中无此特征组合项

<女性，汽车>的含义是女性看汽车广告。可以看到，单特征对应的样本数远大于组合特征对应的样本数。训练时，单特征参数相比交叉项特征参数会学习地更充分。

因此，可以说FM降低了因数据稀疏，导致交叉项参数学习不充分的影响。

2. FM提升了模型预估能力

依然看上面的示例，样本中没有<男性，化妆品>交叉特征，即没有男性看化妆品广告的数据。如果用多项式模型来建模，对应的交叉项参数$w_{\text{男性,化妆品}}$是学不出来的，因为数据中没有对应的共现交叉特征。那么多项式模型就不能对出现的男性看化妆品广告场景给出准确地预估。

FM模型是否能得到交叉项参数$w_{\text{男性,化妆品}}$呢？答案是肯定的。由于FM模型是把交叉项参数用对应的特征隐向量内积表示，这里表示为$w_{\text{男性,化妆品}} = \langle \mathbf{v}_{男性}, \mathbf{v}_{化妆品}\rangle$。

用男性特征隐向量$\mathbf{v}_{男性}$和化妆品特征隐向量$\mathbf{v}_{化妆品}$的内积表示交叉项参数$w_{\text{男性,化妆品}}$。

由于FM学习的参数就是单特征的隐向量，那么男性看化妆品广告的预估结果可以用$\langle \mathbf{v}_{男性}, \mathbf{v}_{化妆品}\rangle$得到。这样，即便训练集中没有出现男性看化妆品广告的样本，FM模型仍然可以用来预估，提升了预估能力。

3. FM提升了参数学习效率

这个显而易见，参数个数由$(n^2 + n + 1)$变为$(nk + n + 1)$个，模型训练复杂度也由$O(m n^2)$变为$O(m n k)$。$m$为训练样本数。对于训练样本和特征数而言，都是线性复杂度。

此外，就FM模型本身而言，它是在多项式模型基础上对参数的计算做了调整，因此也有人把FM模型称为多项式的广义线性模型，也是恰如其分的。

从交互项的角度看，FM仅仅是一个可以表示特征之间交互关系的函数表法式，可以推广到更高阶形式，即将多个互异特征分量之间的关联信息考虑进来。例如在广告业务场景中，如果考虑User-Ad-Context三个维度特征之间的关系，在FM模型中对应的degree为3。

最后一句话总结，FM最大特点和优势：

FM模型对稀疏数据有更好的学习能力，通过交互项可以学习特征之间的关联关系，并且保证了学习效率和预估能力。

场感知分解机

场感知分解机器（Field-aware Factorization Machine ，简称FFM）最初的概念来自于Yu-Chin Juan与其比赛队员，它们借鉴了辣子Michael Jahrer的论文中field概念，提出了FM的升级版模型。

通过引入field的概念，FFM吧相同性质的特征归于同一个field。在FM开头one-hot编码中提到用于访问的channel，编码生成了10个数值型特征，这10个特征都是用于说明用户PV时对应的channel类别，因此可以将其放在同一个field中。那么，我们可以把同一个categorical特征经过one-hot编码生成的数值型特征都可以放在同一个field中。

同一个categorical特征可以包括用户属性信息（年龄、性别、职业、收入、地域等），用户行为信息（兴趣、偏好、时间等），上下文信息（位置、内容等）以及其它信息（天气、交通等）。

在FFM中，每一维特征$x_i$，针对其它特征的每一种”field” $f_j$，都会学习一个隐向量$\mathbf{v}_{i,f_j}$。因此，隐向量不仅与特征相关，也与field相关。

假设每条样本的$n$个特征属于$f$个field，那么FFM的二次项有$nf$个隐向量。而在FM模型中，每一维特征的隐向量只有一个。因此可以吧FM看作是FFM的特例，即把所有的特征都归属到一个field是的FFM模型。根据FFM的field敏感特性，可以导出其模型表达式：

$$
\hat{y}(\mathbf{x}) := w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle \mathbf{v}_{i,\,f_j}, \mathbf{v}_{j,\,f_i} \rangle x_i x_j \qquad(ml.1.9.5)
$$

其中，$f_j$是第$j$个特征所属的field。如果隐向量的长度为$k$，那么FFM的二交叉项参数就有$nfk$个，远多于FM模型的$nk$个。此外，由于隐向量与field相关，FFM的交叉项并不能够像FM那样做化简，其预测复杂度为$O(kn^2)$。

这里以NTU_FFM.pdf和美团－深入FFM原理与实践都提到的例子，给出FFM－Fields特征组合的工作过程。

给出一下输入数据：

User Movie Genre Price

YuChin 3Idiots Comedy, Drama $9.99

Price是数值型特征，实际应用中通常会把价格划分为若干个区间（即连续特征离散化），然后再one-hot编码，这里假设$9.99对应的离散化区间tag为”2”。当然不是所有的连续型特征都要做离散化，比如某广告位、某类广告／商品、抑或某类人群统计的历史CTR（pseudo－CTR）通常无需做离散化。

该条记录可以编码为5个数值特征，即User^YuChin, Movie^3Idiots, Genre^Comedy, Genre^Drama, Price^2。其中Genre^Comedy, Genre^Drama属于同一个field。为了说明FFM的样本格式，我们把所有的特征和对应的field映射成整数编号。

Field Name Field Index Feature Name Feature Index

User 1 User^YuChin 1

Movie 2 Movie^3Idiots 2

Genre 3 Genre^Comedy 3

－－ Genre^Drama 4

Price 4 Price^2 5

那么，FFM所有的（二阶）组合特征共有10项（$\mathbf{C}_{5}^{2} = \frac{5 \times 4}{ 2!}= 10$），即为：

其中，红色表示Field编码，蓝色表示Feature编码，绿色表示样本的组合特征取值（离散化后的结果）。二阶交叉项的系数是通过与Field相关的隐向量的内积得到的。如果单特征有n个，全部做二阶特征组合的话，会有$\mathbf{C}_{n}^{2} = \frac{n(n-1)}{2}$个。

User	Movie	Genre	Price
YuChin	3Idiots	Comedy, Drama	$9.99

Field Name	Field Index	Feature Name	Feature Index
User	1	`User^YuChin`	1
Movie	2	`Movie^3Idiots`	2
Genre	3	`Genre^Comedy`	3
－	－	`Genre^Drama`	4
Price	4	`Price^2`	5

FFM应用场景

在我们的广告业务系统、商业推荐以及自媒体－推荐系统中，FFM模型作为点击预估系统中的核心算法之一，用于预估广告、商品、文章的点击率（CTR）和转化率（CVR）。

在鄙司广告算法团队，点击预估系统已成为基础设施，支持并服务于不同的业务线和应用场景。预估模型都是离线训练，然后定时更新到线上实时计算，因此预估问题最大的差异就体现在数据场景和特征工程。以广告的点击率为例，特征主要分为如下几类：

用户属性与行为特征：
广告特征：
上下文环境特征：

为了使用开源的FFM模型，所以的特征必须转化为field_id:feat_id:value格式，其中field_id表示特征所属field的编号，feat_id表示特征编号，value为特征取值。数值型的特征如果无需离散化，只需分配单独的field编号即可，如历史pseudo-ctr。categorical特征需要经过one-hot编码转化为数值型，编码产生的所有特征同属于一个field，特征value只能是0/1, 如用户年龄区间、性别、兴趣、人群等。

开源工具FFM使用时，注意事项（参考新浪广告算法组的实战经验和美团－深入FFM原理与实践）:

样本归一化：
特征归一化：
省略0值特征：

回归、分类、排序等。推荐算法，预估模型（如CTR预估等）

参考资料

Sina广告点击预估系统实践
FM、FFM相关Paper、技术博客
http://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html

更多信息请关注：计算广告与机器学习－CAML 技术共享平台